Discuss the model of the image degradation and restoration process
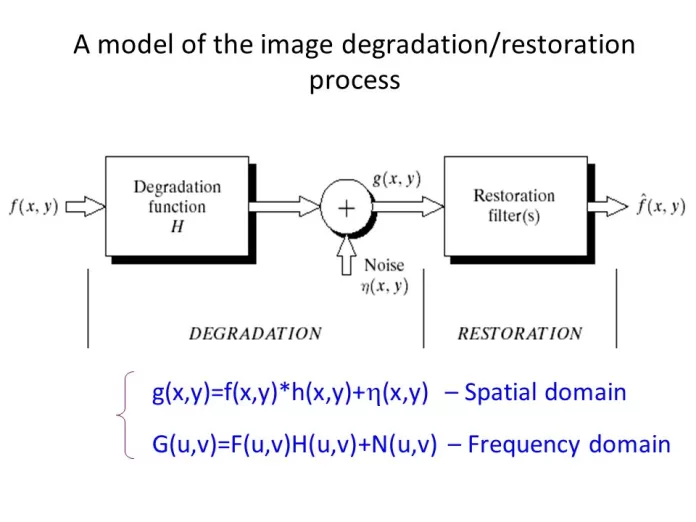
The image degradation and restoration process can be modeled as a mathematical function that transforms a high-quality image into a degraded image, and another function that restores the degraded image back to its original form.
The degradation process can be modeled as a linear transformation of the image, where the image is convolved with a degradation kernel, followed by the addition of noise. This can be represented mathematically as:
Degraded Image = Original Image * Degradation Kernel + Noise
The restoration process aims to undo the degradation and recover the original image as much as possible. This is typically done by finding the inverse of the degradation kernel and applying it to the degraded image. However, since the degradation kernel is often unknown or ill-conditioned, this approach may not produce good results. Therefore, other methods such as regularization and optimization are used to restore the degraded image.
The restoration process can be modeled as an optimization problem, where the goal is to find the solution that minimizes the difference between the degraded image and the restored image. This can be represented mathematically as:
Restored Image = argmin ||Degraded Image – Restored Image|| + Regularization Term
The regularization term is used to enforce certain constraints on the solution, such as smoothness, sharpness, or sparsity. This helps to prevent overfitting and ensure that the solution is reasonable.
Overall, the image degradation and restoration process can be modeled as a mathematical function that transforms a high-quality image into a degraded image, and another function that restores the degraded image back to its original form by minimizing the difference between the degraded image and the restored image, subject to certain constraints.