Bernoulli Equation
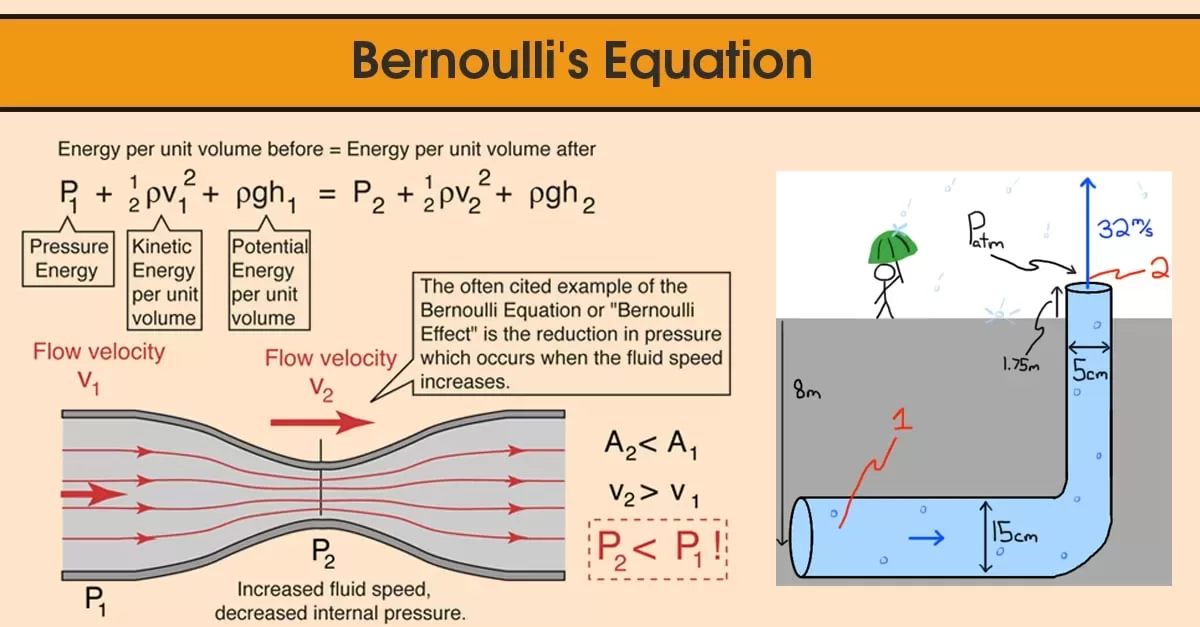
The Bernoulli equation is a mathematical equation that describes the relationship between the velocity and pressure of a moving fluid. It is named after the Swiss mathematician Daniel Bernoulli, who derived the equation in the 18th century.
The Bernoulli equation states that the total energy of a fluid in a system is equal to the sum of its kinetic energy, potential energy, and internal energy. It is commonly used to analyze fluid flow in systems such as pipes, tanks, and channels, and is often used to predict the behavior of fluids under different conditions.
The general form of the Bernoulli equation is:
P + 1/2rhov^2 + rhogh = constant
Where:
P is the pressure of the fluid rho is the density of the fluid v is the velocity of the fluid g is the acceleration due to gravity h is the height of the fluid above a reference point
The Bernoulli equation is often used to predict the behavior of fluids in situations such as the flow of air over an airplane wing or the flow of water in a pipe. It is also commonly used in engineering and physics to analyze the performance of various types of fluid systems.
Applications of Bernoulli Equation
The Bernoulli equation has a wide range of applications in various fields, including engineering, physics, and fluid mechanics. Some of the most common applications of the Bernoulli equation include:
- Analysis of fluid flow in pipes and channels: The Bernoulli equation can be used to predict the flow rate, pressure, and velocity of fluids in pipes and channels. It is commonly used in the design of pipelines and other types of fluid handling systems.
- Analysis of airflow over an airplane wing: The Bernoulli equation is used to predict the lift force generated by an airplane wing, which is important for the stability and performance of the aircraft.
- Analysis of fluid flow in tanks and reservoirs: The Bernoulli equation can be used to predict the behavior of fluids in tanks and reservoirs, including the level of the fluid and the pressure at different points in the system.
- Analysis of water flow in rivers and streams: The Bernoulli equation can be used to predict the flow rate and velocity of water in rivers and streams, which is important for the design of hydroelectric power plants and other water-based systems.
- Analysis of fluid flow in pumps and compressors: The Bernoulli equation is commonly used to predict the performance of pumps and compressors, which are used to move fluids in a variety of applications.
- Analysis of fluid flow in medical devices: The Bernoulli equation is often used to design and analyze the performance of medical devices such as ventilators, which rely on the flow of air to function properly.
Example of Bernoulli’s Equation
Here is an example of how the Bernoulli equation can be used to analyze fluid flow:
Suppose we have a tank of water with a height of 2 meters. At the bottom of the tank, there is a valve that controls the flow of water out of the tank. The valve is connected to a pipe with a diameter of 0.1 meters, which carries the water to a lower elevation.
We can use the Bernoulli equation to predict the flow rate and velocity of the water as it exits the pipe. The general form of the Bernoulli equation is:
P + 1/2rhov^2 + rhogh = constant
Where:
P is the pressure of the fluid rho is the density of the water v is the velocity of the water g is the acceleration due to gravity h is the height of the water above a reference point
To solve this problem, we need to know the pressure and velocity of the water at the bottom of the tank (point 1) and at the end of the pipe (point 2). We can assume that the pressure at point 1 is atmospheric pressure (101,325 Pa) and the velocity of the water at point 1 is zero, since it is not moving.
At the end of the pipe, the pressure is also atmospheric pressure, since the water has reached a lower elevation. The velocity of the water at the end of the pipe will depend on the flow rate and the cross-sectional area of the pipe.
Using the Bernoulli equation, we can solve for the velocity of the water at the end of the pipe:
P1 + 1/2rhov1^2 + rhogh1 = P2 + 1/2rhov2^2 + rhogh2
Substituting the known values into the equation, we get:
101,325 Pa + 0 + (1000 kg/m^3)(9.81 m/s^2)(2 m) = 101,325 Pa + 1/2*(1000 kg/m^3)v2^2 + (1000 kg/m^3)(9.81 m/s^2)*0
Solving for v2, we find that the velocity of the water at the end of the pipe is approximately 3.53 m/s.
This example shows how the Bernoulli equation can be used to predict the flow rate and velocity of a fluid in a system. It is a useful tool for understanding and predicting the behavior of fluids in various types of systems.
Limitation of Bernoulli Equation
There are several limitations to the Bernoulli equation, which should be considered when using it to analyze fluid flow:
- The Bernoulli equation assumes that the fluid is incompressible, which means that its density remains constant regardless of pressure or temperature. This assumption is not always valid, particularly for gases and high-velocity fluids.
- The Bernoulli equation assumes that the fluid is flowing smoothly and without any significant friction or viscous effects. This assumption is not always valid, particularly for fluids flowing through rough or irregular surfaces.
- The Bernoulli equation assumes that the fluid is flowing in a straight line and is not affected by any external forces such as gravity or friction. This assumption is not always valid, particularly for fluids flowing through complex or curved paths.
- The Bernoulli equation does not take into account the effects of heat transfer or chemical reactions on the fluid. These factors can significantly affect the behavior of the fluid and should be considered in more advanced analyses.
- The Bernoulli equation assumes that the fluid has a constant velocity and does not account for changes in velocity over time. This assumption is not always valid, particularly for fluids flowing through complex or dynamic systems.
Overall, the Bernoulli equation is a useful tool for analyzing fluid flow, but it should be used with caution and in conjunction with other analysis techniques when necessary.
If you have any questions, feel free to ask in the comments below. I try my best to respond to every comment that comes my way. If for any reason you don’t get a response, feel free to ask me on Twitter, and Facebook, and if you want to follow me on those social media links as well to see different pictures and just talk about different things going on in the tech world.